競歩における階層的モデル

DC3 佐藤 高嶺

　RIKUPEDIAをご覧の皆様，あけましておめでとうございます．DC3の佐藤です．2021年もRIKUPEDIAを何卒よろしくお願いいたします． 　昨年はコロナウイルスの影響で競技会が少なく，多くの競技者たちにとって厳しい一年となったかと思います．特に試合数がもともと少ない競歩競技者たちには一層厳しい年となりました．しかしながら，そんな中でも5000m競歩と10000m競歩では日本記録が誕生するなど，競歩競技者たちは昨年も非常に高いパフォーマンスを発揮していたように思います．さて，今回のコラムでは，競歩における高いパフォーマンスはいかにして達成されるのかについてパフォーマンス構造の視点から考えてみたいと思います．

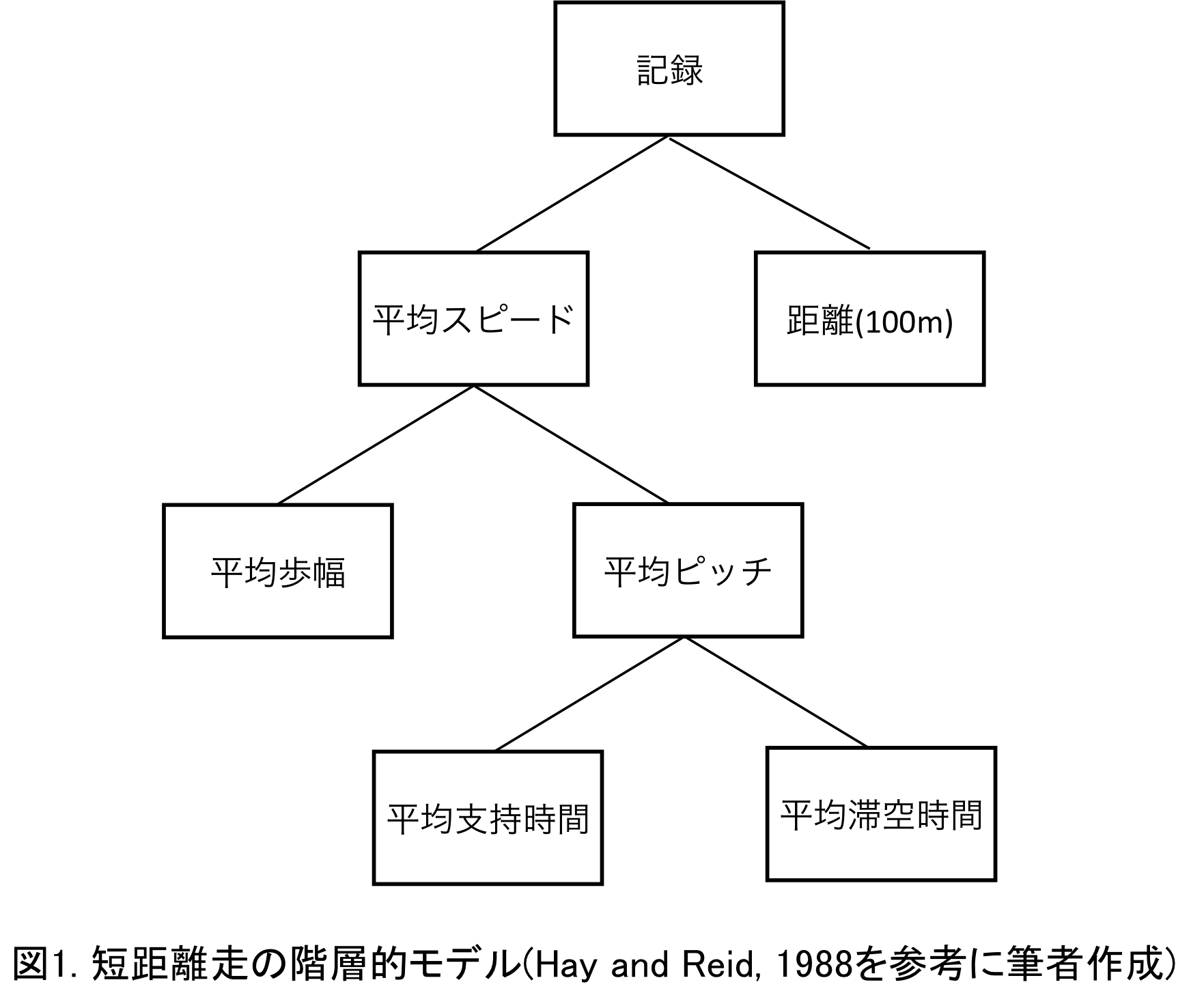
これまで水泳や陸上といった様々な競技におけるパフォーマンス構造が検討され，図1に示すような階層的モデルが示されてきました(Grimston and Hay, 1986 ; Hay and Yu, 1995)．このような階層的モデルでは，はじめにその競技における主要な目標や結果を決め，その後，それに影響する要因を検討し，掘り下げていきます．図1は短距離走における階層的モデルになります(Hay and Reid, 1988)．このモデルでは，パフォーマンス結果である競技記録をはじめに設定し，それを決める要因を平均スピードと距離としており，さらに細かく要因を検討しています．このようなバイオメカニクス的変数を用いた階層的モデルは，変数間の相互関係の評価を可能にし，パフォーマンス改善のために必要な部分やパフォーマンスの制限要因となる部分を特定することにつながり，指導者にとって非常に実用的なものと言えます(Hanley, 2014)．

　 　

競歩における階層的モデル

図2はHanley(2014)が作成した，競歩における階層的モデルです．この競歩のモデルの特徴はレース結果を決める要因に競歩特有のルールに従っていることが内包されている点です．このことは競歩におけるパフォーマンスを高めるには，走種目のように単に歩行スピードを高めるだけではなく，同時に，ルールに沿った動きで歩くことも求められることを意味しています．実際，個人内での歩行スピードの高まりとともに，ロス・オブ・コンタクトの有無を決定する滞空時間の高まりが報告されていることから(Pavei and La Torre, 2016)，歩行スピードだけを追求してしまった場合には，失格となり，レース結果が残らない可能性があります．

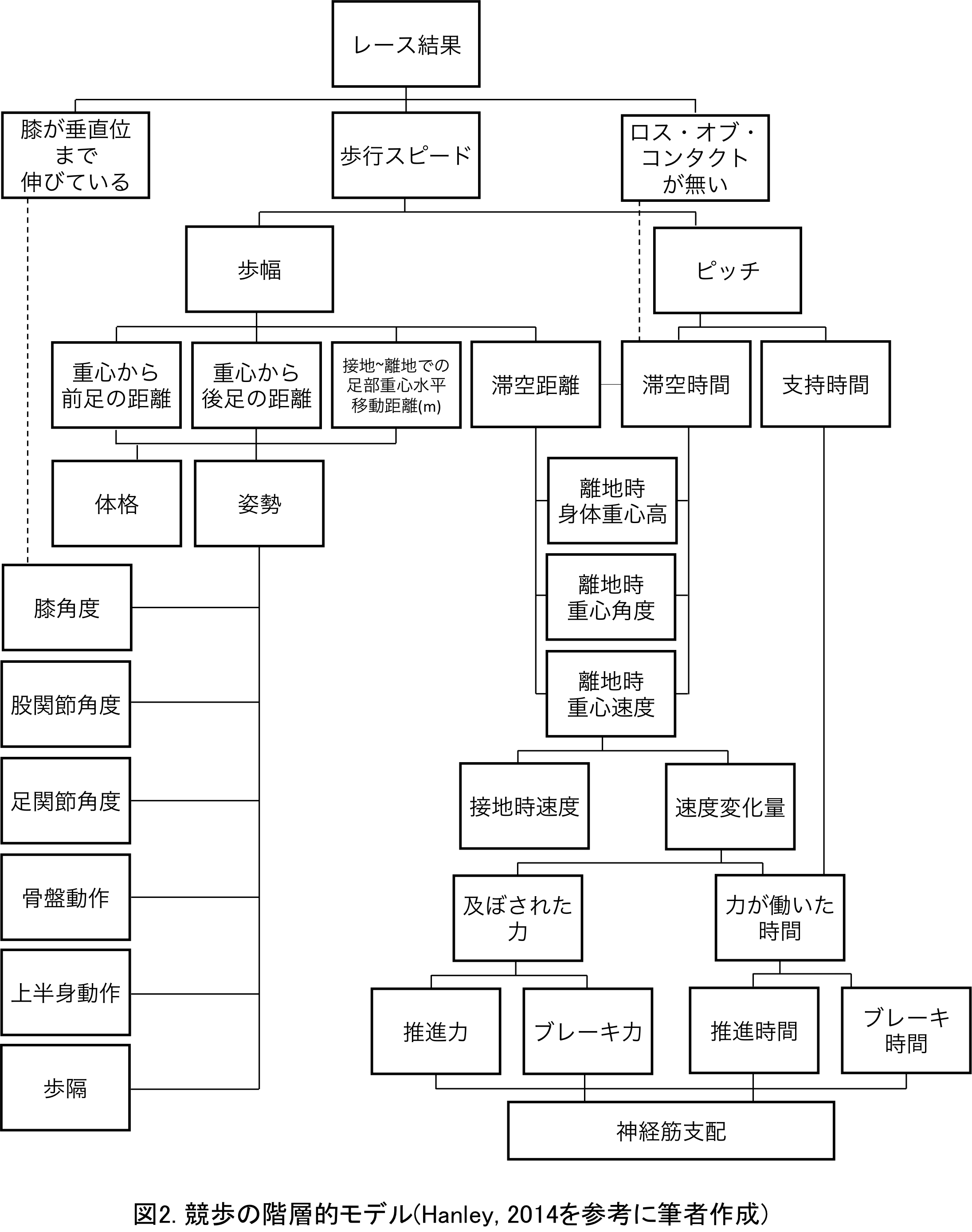
しかしながら，ルールに従った動きが求められつつも，やはり高いパフォーマンスを達成するためには，高い歩行スピードの獲得が必要となります．この歩行スピードを決定する要因は歩幅とピッチとなっており，これら2つを高めることが歩行スピードを高めることになります(Hanley, 2014)．これら2つの要因は更に細かい要因によって決定されており，様々な要因が関係し合いながら競歩のパフォーマンスが成り立っていることがわかります． 　

Hanley(2014)は自身の博士論文の中でこのモデルを作成していますが，それぞれの要因間がどの程度の関係性を持っているのかまでは検討していません．そこで今回は，ここで示された要因間に実際どの程度の関係があるのかを見ていきたいと思います．

要因間における相関関係

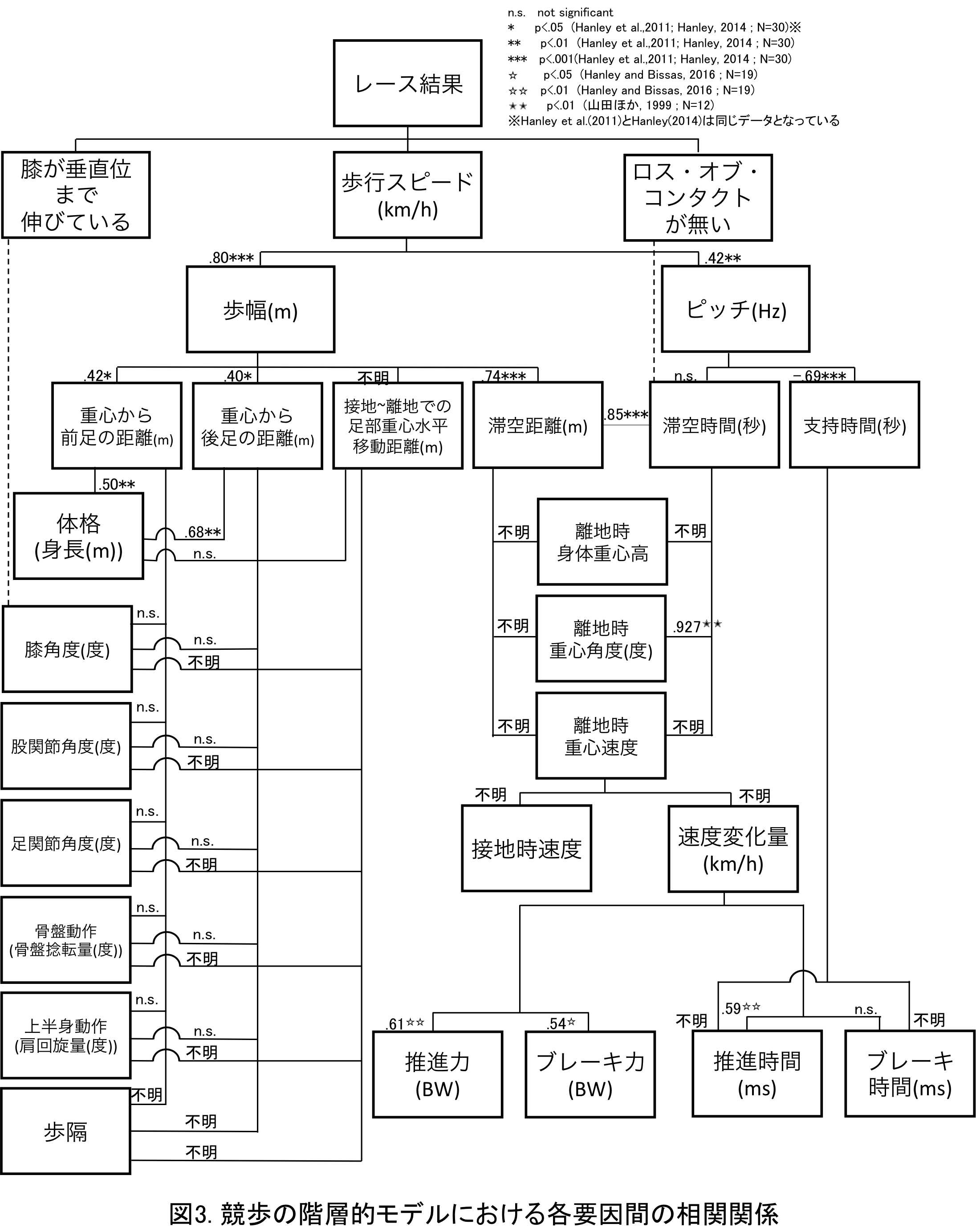
これまで複数の論文において断片的ではありますが，図2のモデル内の要因間の相関関係が検討されてきています(Hanley, 2011 ; Hanley, 2014 ; Hanley and Bissas, 2016 ; 山田ほか, 1999)．これらの論文は，レースペースで歩いた際の歩行を分析しており，競歩競技者たちの実際のレースでの動きや力について検討していると仮定できます．

図2のモデル内の要因の内，これまでに相関関係が報告されている要因間に相関係数をそれぞれ示したものが図3になります．これまで関係が検討されていない，あるいはその結果が論文に示されていない要因間については不明と示しました．また，図2のモデル内の要因の内，個々の変数として曖昧であった「姿勢」，「及ぼされた力」，「力が働いた時間」，「神経筋支配」は取り除き，1つ下の要因がある場合には，一つ上のレベルの要因につなぎ直しました．さらに，上記の論文内で検討が行われている変数をもとに「体格」を身長，「骨盤動作」を骨盤捻転量，「上半身動作」を肩回旋量として検討しました．なお，キネマティクス的パラメータ(歩幅や関節角度など)の要因間の関係や身長と歩幅に関する変数との関係は，男性競技者におけるものとなっているため，女性競技者の場合は関係が異なることに注意してください．

図3を見ると，歩行スピードが大きいほど歩幅も大きく，ピッチも高い関係にあることがわかります．相関係数がそれぞれr=.80，r=42であることから，Hanley(2014)は男子においては大きな歩行スピードの獲得は歩幅によるところが大きいと推察しています．また，Pavei et al.(2014)は複数の先行研究のデータをもとに回帰分析を行い，スピード上昇に伴う変数の変化はピッチよりも歩幅のほうが大きいことを示しており，このことからも大きな歩行スピード獲得には歩幅がより大きな影響を与えている可能性が伺えます．次に，滞空時間を見ると，滞空時間が長いほど歩幅の構成要素である滞空距離も大きい関係にあり，滞空距離が大きいほど歩幅も大きい関係にあることがわかります．これらのことから，Hanley(2014)は，一流競歩競技者たちの大きな歩幅の獲得は，長い滞空時間によるところが大きいことを指摘し，滞空局面がなかった場合には，競技者たちはかなり遅かっただろうと推測しています．ただし，先に述べたように歩行スピードだけを追求してしまった場合には，失格となり，レース結果が残らない可能性があります．実際，Hanley and Bissas(2016)は，滞空時間が長すぎることは失格のリスクを高めるため，歩行速度を高める際に，故意に滞空時間を伸ばそうとすることは望ましくないことを指摘しています．競歩競技のパフォーメンスが判定の上で成り立っていることは決して忘れないで下さい．

このようにモデル内のそれぞれの関係について検討することで，競歩競技者の高いパフォーマンス(高い歩行スピード)がどのように達成(獲得)されているのかが見えてくるかと思います．これによりパフォーマンス向上のための着眼点が指導者のみならず競技者にも示されるのではないでしょうか．

今後の課題

ここまでモデル内の要因間の相関関係の一部を取り上げて，競歩のパフォーマンスについて考えてきましたが，相関関係はあくまでも要因相互の関係を示すものであるため，その因果関係については明らかになりません．そのため，実質的には歩行スピードに有意に貢献している要因，その貢献度についてはわかっていません．また，要因間の関係について，他の要因から受ける影響などについても考慮がなされていません．例えば，図3の滞空時間とピッチとの間には有意な関係は認められていませんが，Hanley et al.(2011)における滞空時間と支持時間にはr=-.77と負の相関があり，支持時間とピッチにもr=-.69と負の相関があります．このことから滞空時間とピッチとの関係には，支持時間からの影響が加わっている可能性が考えられます．そこで，Hanley et al.(2011)で示された相関係数をもとに，支持時間からの影響を排除した際の滞空時間とピッチとの偏相関係数を計算すると，r=-.65となり，負の相関があることがわかります．このように，他の要因からの影響を考慮し，要因間の因果関係を明らかにすることで，競歩におけるパフォーマンス構造はより具体的なものとなってくるのではないかと考えています．そのモデルの作成が現在の私の研究課題であるため，競技現場に携わる方々にとって有益となるモデルを提示できるよう，今後も研究に励みたいと思います．