箱根駅伝の勝負を決する区間とは？—統計を用いたレースの分析—

MC2　関　慶太郎

Rikupediaをご覧の皆様，明けましておめでとうございます．MC2の関です．陸上界は駅伝・ロードレースのシーズン真っ盛りですが，いかがお過ごしでしょうか．駅伝と言えば，つい先日行われた第91回東京箱根間往復大学駅伝競走（箱根駅伝）において，青山学院大学が圧倒的な大会新記録で初優勝を飾りました．近年の箱根駅伝では，山登りの5区で勝負が決すると言われることも多々ありますが，果たして本当にそうなのでしょうか．そこで，今回は簡単な統計手法を用いて第91回箱根駅伝を分析してみたいと思います．なお，今回の分析ではコースの距離や特徴（高低差や風）などは考慮せず，区間ごとの平均走速度を用いて検討します．

まず，図1にはそれぞれの区間の平均走速度と標準偏差，そして優勝した青山学院大学の選手の走速度（緑丸）と区間賞を獲得した選手の走速度（赤丸）を示しました．平均走速度でみると，山登りである5区は明らかに走速度の遅い区間であることがわかります．それと同時に5区で区間賞を獲得した，青山学院大学の神野大地選手の走速度が周囲の選手に比べて圧倒的に速かったことがわかります．

次に，各区間の走速度と総合記録との相関関係をみていきます．各区間の走速度と総合記録との間の関係を散布図として図2に示しました．回帰直線を引いている区間では，走速度と総合記録との間に有意な相関関係が認められたことを示しています．また，散布図に書き込んでいる「r」は相関係数を示しており，-1に近いほど相関関係が強く，0に近いほど相関関係が弱いことを表しています．

全区間の中で最も強い相関関係が認められたのは，2区（r=-0.77）でした．2区において走速度と総合記録との間に最も強い相関関係が認められたことは，花の2区とも言われるように各チームのエースが揃う区間であることを示していると言えるでしょう．2区に次いで強い相関関係が認められたのは，7区（r=-0.74），9区（r=-0.73）でした．

巷で勝負が決すると言われている，5区の相関係数は-0.53を示しており，強い相関関係が認められるとは言い難いものでした．これは多くの方にとって意外な結果なのではないでしょうか．また，5区の結果は区間賞を獲得した神野選手（図2．緑丸）が相関関係に大きく影響を与えている可能性があるため，この選手を除いて相関関係を検討してみると，相関係数は-0.28となり，有意な相関関係は認められませんでした．したがって，5区の記録が良いことは必ずしも総合記録が良いとは限らないことを示唆しています．また，相関関係が弱いということは，この区間では大きな差をつけることが難しいとも考えられます．こういった結果は，この区間が他の区間と比較して特殊であることを端的に表していると言えるでしょう．これらのことから，上位入賞を目標とする場合，この区間では大きな差をつけることよりも，まずは無難につなぐことが重要になってくるのではないでしょうか．一方で，5区で区間賞を獲得した神野選手は一般的な傾向を大きく逸脱した記録を示しており，これが優勝の決め手になった可能性は否定できません．差をつけることが難しい区間で突出した成績を残せることは，優勝するためには必要なことなのかもしれません．勝負が大きく分かれるように見える往路の意外な結果に対して，復路の6区から10区では，すべての区間で走速度と総合記録との間に有意な相関関係が認められました．これは，復路の成績が総合成績に大きく影響することを示唆しています．言い換えれば，往路ではどのチームも強い選手を起用できますが，本当に強いチームは復路にも強い選手を起用できていることを示していると考えられます．

近年の箱根駅伝は山登り（5区）で勝負が決まってしまって，復路が面白くないという意見も耳にするようになりました．しかしながら，復路の5区間の走速度と総合記録には有意な相関関係が認められ，結果に大きく影響していることがわかりました．復路では，見た目の順位と実際の順位が異なることから，その面白みが伝わりにくい側面もあるかもしれませんが，このような結果を踏まえてレースを見返してみると，また新たな発見があるかもしれません．なお，冒頭でも述べましたが，今回の分析は各区間の走速度のみに着目したものであり，他の多くの要因を考慮していませんので，あくまでもひとつの見方として捉えていただければ幸いです．

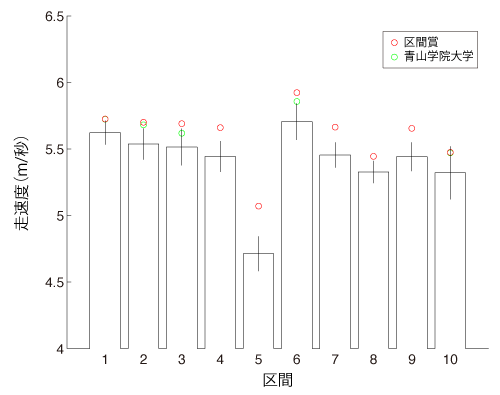
図1．各区間の走速度

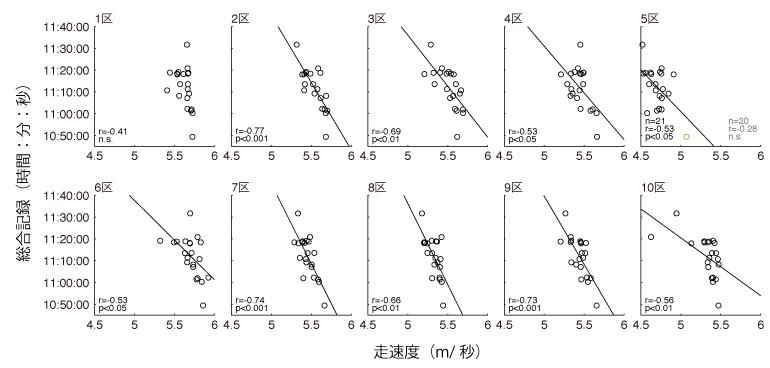
図2．各区間の走速度と総合記録との関係