「体重が軽ければ跳べる」は本当か！？

MC1 衛藤　昂

今回のコラムは，大学院1年 走高跳専門の衛藤昂が担当致します．私は昨年度まで鈴鹿高専（三重）に所属していましたが，4月に大学院に入学しました．7年間工学を専門にし，現在は体育を専門にしています．私も「工学から体育に行く人はいないだろう」と思っていましたが，意外と他分野からの進学者が多く，その存在に励まされながら日々過ごしております．

初回は，論文紹介ではなく「最近ふと気づいたこと」について書きます．では，タイトルの「体重が軽ければ跳べるは本当か!?」を高校物理で考えてみます．

物体が仕事をする能力を持つとき，物体はエネルギーを持つといいます．一般に，運動している物体がもつエネルギーを運動エネルギーK（「K=mv2/2」m:質量，v:速度）といいます．また，高いところにある物体は，質量と高さに応じた位置エネルギーU（「U=mgh」m:質量，g:重力加速度，h:高さ）を持ちます．そして，これらのエネルギーは，力学的エネルギー保存則より，

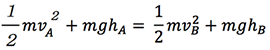
（m:質量，vA:地点Aでの速度，hA:地点Aの高さ，vB:地点Bでの速度，hB：地点Bの高さ，g:重力加速度）

と表すことができます1)．

走高跳に戻ります．ここに踏切局面を当てはめると,
m:人間の体重[kg]，vA:離地時の鉛直速度[m/s]，vB:頂点での鉛直速度[m/s]
g:重力加速度[m/s2]，hA:踏切時の重心位置[m]，hB:頂点での重心位置[m]
となります．

vB=0（頂点では上向きの力が働かない）のため，

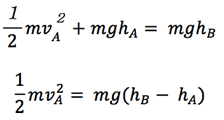
この式の右辺「mgh」に注目すると，「質量mを小さくすれば少ないエネルギーで上に行けるじゃないか！」と考えられます．しかし，左辺「mv2」に注目すると，mが小さくなると，「地面に加えられるエネルギー」＝「地面から跳ね返ってくるエネルギー」（作用反作用の法則1)）が小さくなってしまいます．

さらに，mを削除しhの式にすると，

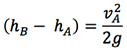
踏切時の鉛直速度が高い選手は，水平速度も高い傾向にあります2)．従って，助走速度を上げれば高く跳べるのではないかと考えられますが，踏切において水平速度を鉛直速度に変換する“踏切技術”“関節及び身体の強さ”がないと高さは獲得できません．走高跳においては，スプリントの強化と共に，それを跳ね返せる身体を作り上げることが重要であると思います．

今回は,物理的解釈を行いました．走高跳は様々な角度から研究され，非常に多くの論文があります．例えば,「なぜハイジャンパーは曲線助走をするのか」「踏切時における足関節の変形」「背面跳よりも効率的な跳躍スタイル」など興味深いものばかりです．私はまだまだ勉強不足ですが，「走高跳って面白いな！」と思っていただけるようなコラムを目指しますので，今後ともよろしくお願い致します．